Important Information
This section contains useful information for developers/users who want to
General Philosophy
The implementation and organization of the library is guided by
Low code duplication
The requirement that a new map/cost/algorithm should need one to edit/create only one file
The existence of a solution to new needs (i.e., few hard constraints to respect in implementations)
The systematic choice between fast but memory consuming and memory efficient but slower.
Hierarchy of Classes
The library is based on the four abstract classes Map, LinOp, Cost, and Opti. All other classes
inherit from them. Note that nonlinear operators inherit directly from the
Map class since they do not require specific attributes/methods.
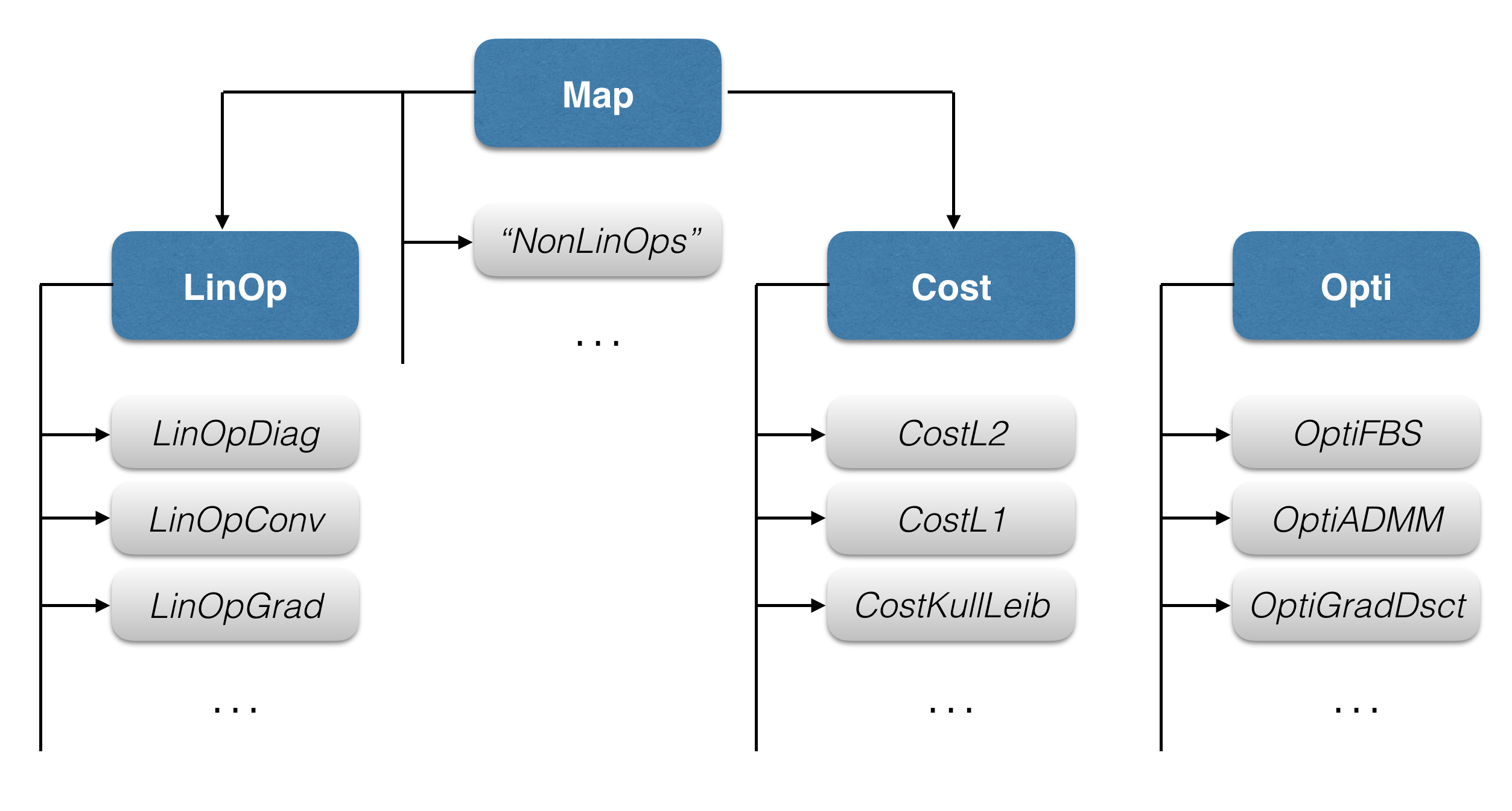
Fig 1. Hierarchy of classes within the GlobalBioIm library.
Interface Methods and Core Methods
Every class (except Opti classes) contains two types of methods
Interface methods are methods that can be called from an instanciated object of the class. They check the size conformity of the input and call the corresponding core method. Morever, they manage the memoize mechanism (see below). Their implementation is done at the level of abstract classes. (To implement a new class, developers do not have to deal with the memoize system as well as to check of input sizes.)
Core methods are methods that contain implementation. Developers only need to implement these methods.
Methods always go by pair (Interface + Core). They have the same name, followed by a “_” symbol for core ones. For instance,
apply()
apply_().
Exception The mtimes() method (i.e., the overloading of the * operator) has no associated core method.
This method calls either apply() or makeComposition(), depending on the
right-hand side of the operation.
Memoize and Precomputation Options
The Map class provides two attributes
memoizeOptsis a structure of booleans with one field per method of the class (default all false). If, for instance, the field memoizeOpts.apply is set to true, the result of theapply()method \(\mathrm{y=Hx}\) is saved. Then, if the next call to theapply()method is for the same \(\mathrm{x}\), the saved value \(\mathrm{y}\) is directly returned without any computation.
doPrecomputationis a boolean (default false). When true, some methods of the instanciated object will be accelerated at the price of a larger memory consumption. It depends on how the implementation of the class has been done. Hence, if one wants to accelerate a method by precomputing some quantities, this has to be done when the doPrecomputation option is activated, and not by default. This offers the possibility to bypass precomputation steps in the presence of memory limitations.
Let us look at some examples. Consider a convolution oprerator LinOpConv
H=LinOpConv(fftn(psf));
H.memoizeOpts.apply=true;
for a given PSF (\(512\times 512 \times 256 \)) and for which we have activated the memoize option of the apply() method.
Then, let us make the following calls to the apply() method:
>> x=rand(size(psf));
>> tic;y=H*x;toc;
Elapsed time is 2.414025 seconds.
>> tic;y=H*x;toc;
Elapsed time is 0.085205 seconds.
>> x(5)=2;
>> tic;y=H*x;toc;
Elapsed time is 2.465424 seconds.
>> tic;y=H*x;toc;
Elapsed time is 0.083087 seconds.
Here, one can appreciate the effect of the memoize option. To observe the effect of the precomputation option,
we instantiate a CostL2 object and combine it with our convolution operator. Moreover, we activate the precomputation option for the resulting CostL2Composition object.
>> y=rand(size(psf));
>> LS=CostL2([],y);
>> F=LS*H;
>> F.doPrecomputation=1;
Let us evaluate the gradient of the cost F at x.
>> x=rand(size(psf));
>> tic;g=F.applyGrad(x);toc;
Elapsed time is 5.236043 seconds.
>> tic;g=F.applyGrad(x);toc;
Elapsed time is 2.554012 seconds.
>> tic;g=F.applyGrad(x);toc;
Elapsed time is 2.572284 seconds.
For a CostL2, when the precomputation option is activated, the gradient is computed using
$$ \nabla F(\mathrm{x})= \mathrm{H^*Hx - H^*y},$$
which allows us to take advantage of a fast implementation of \( \mathrm{H^*H}\) (for the above example, \( \mathrm{H^*H}\) is also a
convolution). Here, at the first call of applyGrad(), the quantity \(\mathrm{H^*y}\) is computed and stored
(hence 4 FFT/IFFT are performed). Then, for all subsequentg calls to applyGrad(), the computation is now reduced to
the application of \( \mathrm{H^*H}\) and requires only 2 FFT/IFFT.
In this example, we computed the gradient 3 times over the same x without activating the memoize option
of the applyGrad() method in order to show the effect of precomputation. Of course, doing new calls to applyGrad()
with the same x after having activated the memoize option produces
>> F.memoizeOpts.applyGrad=true;
>> tic;g=F.applyGrad(x);toc;
Elapsed time is 2.572987 seconds.
>> tic;g=F.applyGrad(x);toc;
Elapsed time is 0.075061 seconds.
Compositions
The library deploys an operator-algebra mechanism that allows for generic implementations. This is made possible
by the methods prefixed by make (i.e., makeComposition_(), makeAdjoint_(), makeHtH_(), makeHHt_()…)
as well as the plus_(), minus_(), and mpower_() methods. By default these methods will instanciate Operations on Maps objects which may lose
properties such as invertibility or speed of implementation (due to the genericity of these classes).
However, developers can reimplement these make methods
in derived classes. For instance, in LinOpConv, one can find
function M = plus_(this,G)
% Reimplemented from parent class :class:`LinOp`.
if isa(G,'LinOpDiag') && G.isScaledIdentity
M=LinOpConv(G.diag+this.mtf,this.isReal,this.index);
elseif isa(G,'LinOpConv')
M=LinOpConv(this.mtf+G.mtf,this.isReal,this.index);
else
M=plus_@LinOp(this,G);
end
end
function M = minus_(this,G)
% Reimplemented from parent class :class:`LinOp`.
if isa(G,'LinOpDiag') && G.isScaledIdentity
M=LinOpDiag(this.mtf-G.diag,this.isReal,this.index);
elseif isa(G,'LinOpConv')
M=LinOpConv(this.mtf-G.mtf,this.isReal,this.index);
else
M=minus_@LinOp(this,G);
end
end
function M = makeHHt_(this)
% Reimplemented from parent class :class:`LinOp`.
M=LinOpConv(abs(this.mtf).^2,this.isReal,this.index);
end
function M = makeHtH_(this)
% Reimplemented from parent class :class:`LinOp`.
M=LinOpConv(abs(this.mtf).^2,this.index);
end
function G = makeComposition_(this, H)
% Reimplemented from parent class :class:`LinOp`
if isa(H, 'LinOpConv')
G = LinOpConv(this.mtf.*H.mtf,this.isReal,this.index);
elseif isa(H,'LinOpDiag') && H.isScaledIdentity
G = LinOpConv(this.mtf.*H.diag,this.isReal,this.index);
else
G = makeComposition_@LinOp(this, H);
end
end
which all instanciate a new LinOpConv with the proper kernel. Hence, considering a LinOpConv,
>> H=LinOpConv(fft2(psf))
H =
LinOpConv with properties:
mtf: [256x256 double]
index: [1 2]
Notindex: []
ndms: 2
isReal: 1
name: 'LinOpConv'
isInvertible: 0
isDifferentiable: 1
sizein: [256 256]
sizeout: [256 256]
norm: 1.0000
memoizeOpts: [1x1 struct]
doPrecomputation: 0
the \(\mathrm{H^*H} \) is also a LinOpConv
>> H'*H
ans =
LinOpConv with properties:
mtf: [256x256 double]
index: [1 2]
Notindex: [1?0 double]
ndms: 2
isReal: 1
name: 'LinOpConv'
isInvertible: 0
isDifferentiable: 1
sizein: [256 256]
sizeout: [256 256]
norm: 0.9999
memoizeOpts: [1x1 struct]
doPrecomputation: 0
and the same holds for the \(\mathrm{H^*H + I} \) operator
>> I=LinOpIdentity(size(psf));
>> H'*H+I
ans =
LinOpConv with properties:
mtf: [256x256 double]
index: [1 2]
Notindex: [1?0 double]
ndms: 2
isReal: 1
name: 'LinOpConv'
isInvertible: 1
isDifferentiable: 1
sizein: [256 256]
sizeout: [256 256]
norm: 1.9999
memoizeOpts: [1x1 struct]
doPrecomputation: 0
which is invertible in comparison to \(\mathrm{H}\) and \(\mathrm{H^*H}\). This combination mechanism allows for generic implementations. For instance, there is a property stating that, given the proximity operator of a convex function \(f\), the proximity operator of \(f(\mathrm{H}\cdot)\), for \(\mathrm{H}\) a semi-orthogonal linear operator (i.e., \(\mathrm{HH^*}= \nu \mathrm{I}\) for \(\nu >0\)), is given by
$$ \mathrm{prox}_{f(\mathrm{H}\cdot)}(\mathrm{x}) = \mathrm{x} + \nu^{-1}\mathrm{H^*} \left( \mathrm{prox}_{\nu f}(\mathrm{Hx}) -\mathrm{Hx} \right). $$
Hence, at the level of CostComposition, one can check if \(\mathrm{H}\) is a semi-orthogonal linear operator
and implement in a generic way the above property. In the constructor,
T=this.H2*this.H2';
if isa(T,'LinOpDiag') && T.isScaledIdentity
if T.diag>0
this.isH2SemiOrtho=true;
this.nu=T.diag;
end
end
and in the applyProx_() implementation
function x=applyProx_(this,z,alpha)
if this.isConvex && this.isH2LinOp && this.isH2SemiOrtho
x = z + 1/this.nu*this.H2.applyAdjoint(this.H1.applyProx(this.H2*z,alpha*this.nu)-this.H2*z);
else
x = applyProx_@Cost(this,z,alpha);
end
end
As a result, in the library, combining any Cost having an implementation of applyProx_() with a LinOp
which is semi-orthogonal (its makeHHt_() returns a LinOpDiag with a constant diagonal) results in a new
Cost which has an implementation of applyProx_().
Important The use of this operator algebra is not the recommended way to implement methods since it creates at each call a new object and may slow iterative algorithms. However, it can be used freely in constructor methods or in other methods as a default implementation.
Deep Copy
By default matlab performs shallow copy of handle objects such as Map and inherited classes.
It means that shallow copied object will share the same properties and memoize system cache during their whole life.
The function copy() perform a deep copy preventing this sharing. Its behavior can be changed by overloading the
method copyElement().
>> H=LinOpConv(fftn(psf));
>> H.memoizeOpts.apply=true; % Activate the memoize cache
>> tic; y =H*x;toc
Elapsed time is 2.117364 seconds.
>> tic; y =H*x;toc
Elapsed time is 0.090888 seconds.
>> B = H; % Shallow copy
>> tic; y =B*x; % H and B share the same memoize cache
Elapsed time is 0.089999 seconds.
>> tic; y =B*z;toc
Elapsed time is 2.250312 seconds.
>> tic; y =H*x;toc
Elapsed time is 2.180036 seconds.
using copy() deep copy:
>> C = copy(H) % Deep Copy
>> tic; y =H*x;toc
Elapsed time is 2.117364 seconds.
>> tic; y =H*x;toc
Elapsed time is 0.090888 seconds.
>> tic; y =C*x;toc
Elapsed time is 2.202259 seconds.
>> tic; y =C*z;toc
Elapsed time is 2.194160 seconds.
>> tic; y =H*x;toc
Elapsed time is 0.097449 seconds.
Auxiliary Utilities
The library contains a folder Util/ with several functions. These include viewers or check functions that give a
first control that an implementation is correct. For instance, the CheckMap function verifies some basic relations
between the different methods implemented in the given Map.
>> H=LinOpConv(fft2(psf));
>> checkMap(H)
-- Checking Map with name LinOpConv--
apply OK
applyJacobianT OK
applyInverse OK
SNR: 296 dB, OK
-- LinOp-specific checks --
applyAdjoint OK
SNR: 306 dB, OK
applyHtH OK
SNR: 318 dB, OK
applyHHt OK
SNR: 331 dB, OK
Provided Templates
Templates for the implementation of new Map, LinOp, Cost, or Opti are provided to help developers.
They can be found under
TemplateMap.m
TemplateLinOp.m
TemplateCost.m
TemplateOpti.m